Introduction Portfolio Management Process:
The article “Portfolio Selection” is the findings of work experience of Harry Markowitz. On august 24, 1927, Harry Markowitz was born in Chicago. The findings depends depend upon the assumptions that discount rates and the anticipated returns portfolio of particular investor. With highest r, an unlimited amount of money would be placed in the security; in the case of shot sales were allowed.
Difficult questions like how investors do or form their probability beliefs are not answered in this paper. For example, the assumption is that the investor would act as if he had probability beliefs concerning these variables. Mostly, we shall expect that the investor could tell, whether he personally considered A more likely than B, B more likely than A, or both equally likely, for any two events (A and B). The investor would possess a system of probability beliefs if he was consistent in his opinions on such matters. It cannot be expected that the investor would be consistent in every detail. However, it shall be expected that investor probability beliefs to be roughly consistent on important matters that have been carefully considered. Even though they are in part subjective the expectations should lead that investor will base his actions upon these probabilities beliefs.
Process of Portfolio:
Portfolio selection process shall be divided in two phases. The first phase of processing of portfolio starts from observation and experience. It ends with beliefs about the future performances of available securities. This article does not discuss this phase so we would progress towards second phase. It starts from the relevant beliefs about future performances and ends with the choice of portfolio.
In 1952, he put forward this model. It assists in the selection of the most efficient by analyzing various possible portfolios of the given securities. By choosing securities that do not move exactly together, the HM model shows investors how to reduce their risk. The HM model is also called Mean-Variance Model (MVM) due to the fact that it is based on expected returns (mean) and the standard deviation (variance) of the various portfolios.
Harry Markowitz made the following assumption while developing the HM model, which were:
- Risk of a portfolio is based on the variability of returns from the said portfolio.
- An investor is risk averse.
- An investor prefers to increase consumption.
- The investor’s utility function is concave and increasing, due to his risk aversion and consumption preference.
- Analysis is based on single period model of investment.
- An investor either maximizes his portfolio return for a given level of risk or maximum return for minimum risk.
- An investor is rational in nature.
To choose the best portfolio from a number of possible portfolios, each with different return and risk, two separate decisions are to be made:
- Determination a set of efficient portfolios.
- Selection of best portfolio out of the efficient set.
Determination a Set of Efficient Portfolios Management Strategies:
A portfolio that gives maximum return for a given risk, or minimum risk for given return is an efficient portfolio. Thus, portfolios are selected as follows:
- An investor will prefer the portfolio with lower risk from the available portfolios that have the same return.
- The investor will prefer the portfolio with higher rate of return from the portfolios that have the same risk level.
Investors would like to have higher return as mostly they are rational. On the other hand, risk-averse investors want to have lower risk.
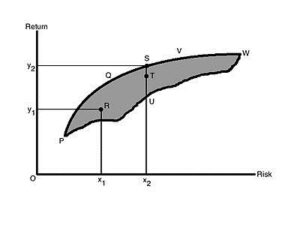
In the figure, all the possible securities are in the shaded area PQSVWUP includes where an investor can invest.
Selection of Best Portfolio out of the Efficient Set:
The risk-return preferences are analyzed for the selection of the best or optimal portfolio. Highly risk averse investor will hold a portfolio on the lower left hand of the frontier, and who is not too risk averse will choose a portfolio on the upper portion of the frontier.
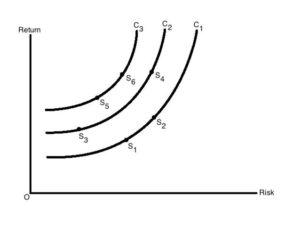
The figure shows the risk-return indifference curve C1, C2 and C3 are shown for the investors. Different combination of risk and return are shown on each of the different points. Investor has same satisfaction on each point. Higher satisfaction or utility is represented at each curve to the left. Maximization of investors’ satisfaction is the overall goal. To achieve this, he moves to a curve that is higher. Investor will move from C2 to C3 as increases his satisfaction at any point between combinations S1 and S2, or S5 and S6.
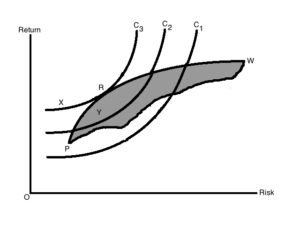
The figure shows optimal portfolio for investor. It is found at the point of tang-ency of the efficient frontier with the indifference curve. This is point where investor can have the highest level of satisfaction. This point marks the highest level of satisfaction the investor can obtain.
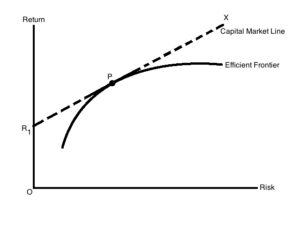
The figure shows the Efficient Frontier and CML with the combination of Risk-Free Return. As government securities have no risk, it is the risk-free return. Efficient portfolios and risk-free returns are at any point on the line R1PX. Capital market is the line R1PX. CML also represents the market equilibrium in the market of portfolios which consists risk-free and risky securities.
The equation of CML is: RP = IRF + (RM – IRF) σP / σM
Where,
- RP = Expected Return of Portfolio
- RM = Return on the Market Portfolio
- IRF = Risk-Free rate of interest
- σM = Standard Deviation of the market portfolio
- σP = Standard Deviation of portfolio
- (RM – IRF)/σM = slope of CML
- (RM – IRF) = measure of the risk premium
- σM = risk of the market portfolio
Therefore, the slope measures the reward per unit of market risk.
Demerits of the HM Mode:
A demerit of the HM Mode requires lots of data to be included. An investor shall obtain estimates of return for all the securities in a portfolio, variances of return, covariance of returns. There are numerous calculations involved that are complicated because from a given set of securities, a very large number of portfolio combinations can be made. The expected return and variance will also have to compute for each security.
